INTERESTING LINKS
Puzzles
Mathematics
Blogs
8. The Wheel of Misfortune
A wheel with 12 sectors has 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0 written on its sectors in the anticlockwise sense. At each trial you are allowed to add or subtract 1 from 2 consecutive sectors. You win the fortune if you finally make all numbers 0. Is it possible to win the fortune?
What if the numbers are in the order 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0?
9. Pick your Stick
You are given a set of sticks; each of them has length equal to some natural number. You randomly pick up two sticks. If the two sticks have equal length, you throw out one of them, and put the other back in the bag. If they are unequal, from the longer you cut off a piece of length same as that of the smaller and throw that away, and put the remaining part and the shorter stick back in the bag.
Now will it always be the case, that you have only one stick in the bag, after a while? What can you say about that one stick, if yes?
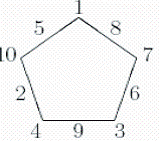
10. The Pentagon
Some positive integers can be arranged along the vertices and sides of a pentagon
(all numbers are diff erent) so that the sum of the three numbers along each side is the same. The diagram shows an arrangement of numbers 1 to 10 with sum
16.Find, with proof, the smallest possible value for a sum and give an example of an
arrangement with that sum.
PREVIOUS PROBLEMS
In this section, you can browse through the problems that have appeared in previous issues of InsIghT, get hints and see the solutions.